Rectangular Prism

In geometry, a rectangular prism is a polyhedron consisting of two congruent lines and parallel bars.  A rectangular prism is also known as a cuboid.  A rectangular prism generally has six rectangle-shaped faces and twelve edges. As it has a cross-section along its length it is known as a prism. Geometry is the study of shapes and configurations of objects. Like any other three-dimensional shape, a rectangular prism has its surface area and volume. The surface area of the prism is the area of the net. The following blog will provide information regarding the definition of a rectangular prism, its types, volume, and surface area of a rectangular prism. 

What is a rectangular prism?

A rectangular primer is a three-dimensional shape consisting of six faces, two at the top, two at the bottom, and four at the lateral faces. All the faces of the prism are rectangular. Therefore, there are three different pairs of identical faces. This shape makes the rectangular prism also known as a cuboid. Some of the most common examples of rectangular prism are geometry boxes, dairies, classrooms, notebooks, rooms, etc. The following figure below is also an example of a rectangular face.

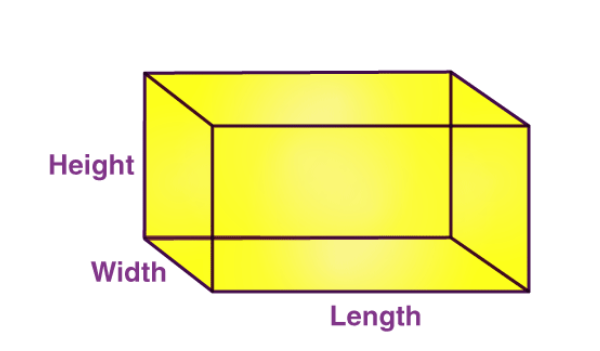
Properties of rectangular prism

• The rectangular prims consist of 12 edges, 6 faces, and 8 vertices. 
• The bottom and top of the rectangular prims are always rectangular. 
• Like any other cuboid, it has three distinct dimensions that are length, width, and height. 
• The opposite pair of faces are always congruent or identical.
• For any right rectangular prism, the lateral faces are always rectangular.
• For an oblique rectangular prism, the lateral faces are in the form of a parallelogram.
• The rectangular prism consists of rectangular cross-sections.
• The shape of a rectangular prism is identical to that of a cuboid. 

Different types of rectangular prism 

There are generally two types of rectangular prism are 

• Right rectangular prism. 
• Oblique rectangular prism.

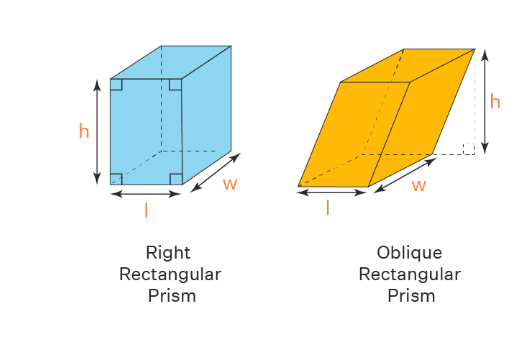
Right rectangular prism

The prism with rectangular bases is known as the right rectangular prism. A right rectangular prism consists of six faces that are rectangular and all the angles involved are right angles. 

• Vertices of right rectangular prism 8
• Edges of rectangular prism 12 
• Faces of rectangular prism 6 (including bases)

Oblique rectangular prism

An oblique rectangular prism consists of bases that are not perpendicular to each other. Any rectangular prism in which the bases are not aligned directly above each other is known as an oblique rectangular prism. 

Formulas of rectangular prims

A rectangular prism is a three-dimensional object. Therefore, it has own its volumes and surface areas. To calculate the surface area and volume of the prism, we have to measure the length of its edges or sides. Let the length be “L”, width be “W”, and height be “H” of the prism. The formulas of different types of rectangular prism are provided below.

1. The formula for the volume of the rectangular prism

The volume of the rectangular prism refers to the measurement of the occupied space of the rectangular prism. The volume of rectangular prims is denoted in cubic units. It can also be said as the number of units required to fill the rectangular prism.

The formula of the rectangular prism is identical to the area of its base times its height. 

Therefore the volume of the rectangular prims can be written as 

“The volume of a rectangular prism = Length x Width x Height cubic units.” 

Volume = l x w x h cubic units

2.The surface area of a rectangular prism

The surface area of the rectangular prims is the amount of exposed area of the prism. The surface area of the rectangular prism is written in square units. The total surface area of the rectangular prism is the sum of the lateral surface area and twice the base area of the rectangular prism.  Therefore the formula for the surface area of a rectangular prism is

“ Total Surface Area of rectangular prism = LSA + 2 (Base area)       [Square units]”

On the other hand, the lateral surface area of the prism is the sum of all the surface areas of the prism taking into consideration the base of the rectangular prism. The lateral surface area of any rectangular prism is equal to the perimeter of the base times the height of the rectangular prism. Therefore, the lateral surface area can be written as  P x h [Square units]. Here 

• P demotes the perimeter of a base
• h is the height of the prism

The perimeter of the rectangular prism is P = 2 (l + w)

Hence the “lateral surface area (LSA), of a rectangular prism = 2 ( l + w ) h square units”

TSA = LSA + 2 (Base Area) = 2 (l + w) h + 2 (l x w) = 2 lh + 2 wh + 2 lw   [Square units] 

Hence the surface area of a rectangular prism is “Surface Area of a rectangular prism = 2 (lh +wh + lw ) Square units”.

Rectangular Prism Net

The net of any prims refers to its surface area. It showcases when we open a prism in the plane, and all its sides can be seen at the same time. When calculating the individual area of all the sides with the net, it will provide the total surface area. The below figure will help in calculating the rectangular prism. 

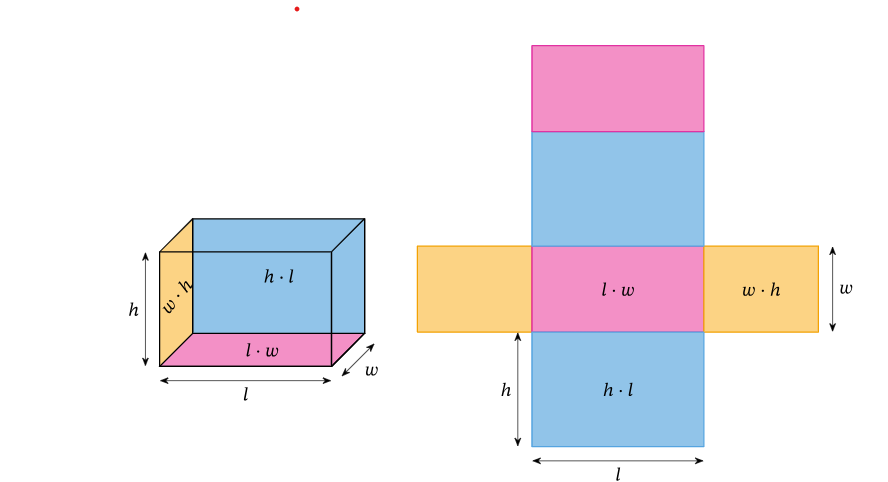
In the above figure, all the different sides of the prism are rectangular. Using the formula present for the area of rectangles, the area of each face can be calculated, and adding them all will give the net of the prism. 

FAQs

Q.1 What is a right rectangular prism?

A right rectangular prism consists of 6 rectangular faces, 8 vertices, and 12 edges. It is also known as a cuboid. 

Q.2 What is the difference between an oblique rectangular prism and a right rectangular prism?

The bases of the oblique rectangular prism are not perpendicular to each other. On the contrary, the bases of the rectangular prism are perpendicular to one another. 

Q.3 What are the different examples of rectangular prism?

Some of the common examples of rectangular prism in real life are books, bricks, doors, etc.

Q.4 What is the volume of a rectangular prism?

The volume of the rectangular prism is the product of its width, length, and height.

Q.5 What is the surface area of the rectangular prism?

The surface area of a rectangular prism is presented by SA = 2 (lh +wh + lw ) Square units.

Q.6 What is the rule for a rectangular prism?

The basic rule for a rectangular prism is that both the bases of the rectangular prism i.e. the top and bottom of the prism should be rectangular. 

Q.7 Is a rectangular prism also a cuboid?

All six faces of the rectangular prism are in rectangular shape identical to a cuboid. Therefore, a rectangular prism is also known as a cuboid.